로지스틱 회귀는 머신러닝과 통계 분석에서 이진 분류 문제를 해결하기 위해 널리 사용되는 기법이다. 오랜 역사를 지니고 있지만, 여전히 실무와 연구에서 중요한 역할을 한다. 로지스틱 회귀는 기본적으로 퍼셉트론 알고리즘의 발전 과정에서 탄생했다.
퍼셉트론(Perceptron) 알고리즘
1957년 미국의 심리학자 프랑크 로젠블라트(Frank Rosenblatt)가 제안한 알고리즘. 퍼셉트론 알고리즘은 신경 세포 뉴런과 유사하게 작동한다. 뉴런이 신호를 받고 임계치를 넘으면 다음 뉴런에 신호를 전달하는 것과 같이, 퍼셉트론은 입력받은 데이터로 값을 계산하고, 계단 함수(step function)를 이용하여 그 값이 임계치 이상이라면 참(True)을, 임계치 미만이라면 거짓(False)을 반환한다.
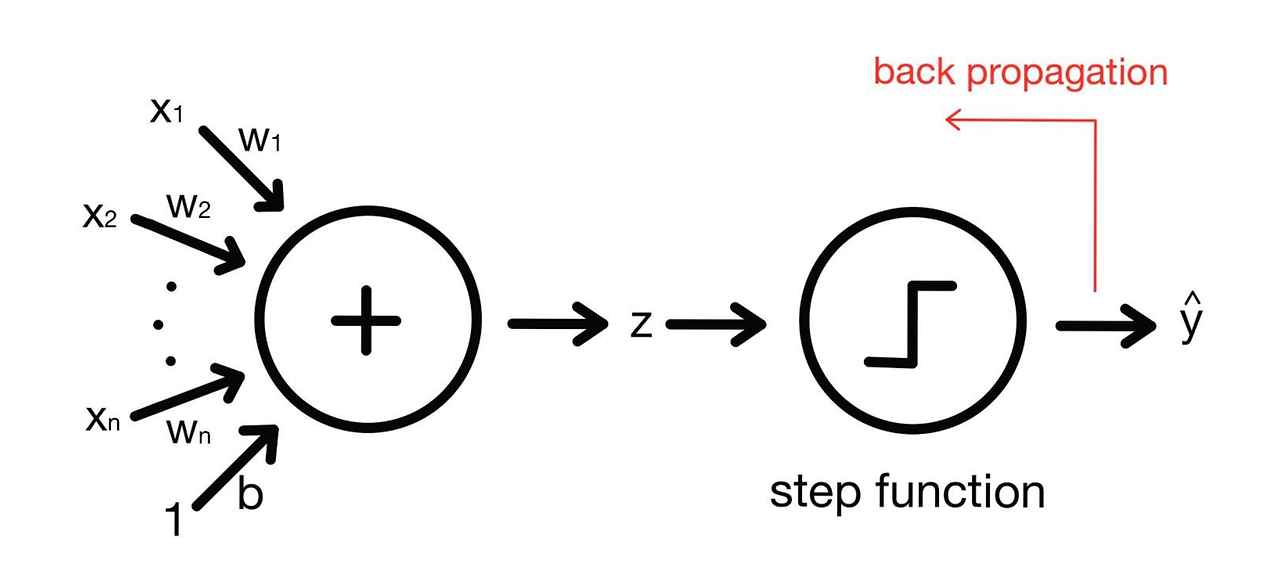
적응 선형 뉴런(Adaptive Linear Neuron)
퍼셉트론은 계단 함수를 통과한뒤에 가중치 업데이트를 수행하는데, 계단 함수를 통과한 값들은 -1과 1이기 때문에 연속적인 손실 함수를 사용할 수 없다는 단점이 있다. 이를 개선한 것이 바로 1960년 버나드 위드로우(Bernard Widrow)와 테드 호프(Tedd Hoff)가 발표한 적응 선형 뉴런(Adaptive Linear Neuron; ALN) 혹은 아달린(Adaline)이다. 적응 선형 뉴런은 계단 함수를 통과하기 전 데이터(선형 방정식을 통해 계산된 값)를 이용하여 가중치를 업데이트하기 때문에 연속적인 손실 함수를 사용할 수 있다.
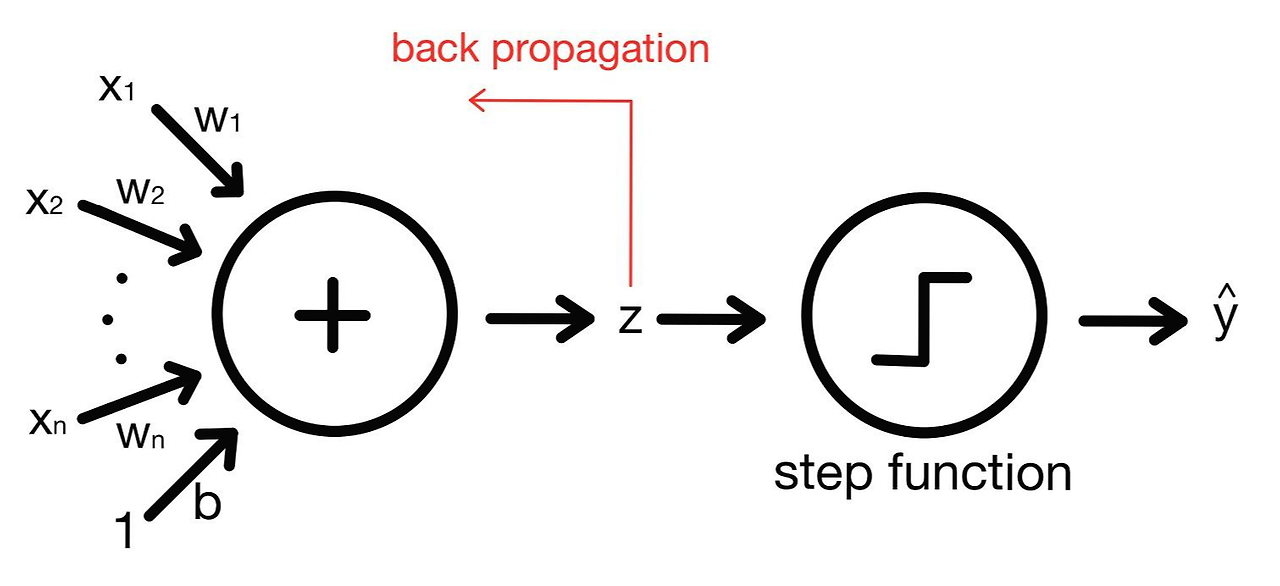
로지스틱 회귀(Logistic Regression)
적응 선형 뉴런에 활성화 함수(Activation function)를 추가한 모델이 바로 로지스틱 회귀(Logistic Regression)이다. 활성화 함수로는 시그모이드 함수(Sigmoid Function)를 사용한다. 로지스틱 회귀 모형의 구조는 아래 그림과 같다.
로지스틱 회귀에 대해 조금 더 자세히 살펴보자. 로지스틱 회귀 모형은 바이너리 분포를 따르는 종속변수 y에 대해, 종속변수의 확률 p와 독립변수 x간 관계를 다음과 같은 선형 방정식으로 설명한다.
$$\log\left(\frac{p}{1-p}\right) = w_{0} + w_{1}x_{1} + w_{2}x_{2} + \cdots + w_{n}x_{n}$$
우변의 선형 방정식 결과는 좌변의 로그 오즈 비율로 표현되며, 값의 범위는 $-\infty$에서 $\infty$이다. 그러나 우리가 얻고자 하는 것은 로그 오즈 비율이 아닌 오즈 비율(p)이다. 이를 0과 1사이의 범위를 갖는 확률로 변환시키기 위해, 아래와 같은 시그모이드 함수를 사용한다. 즉, 시그모이드 함수는 로짓 링크 함수의 역함수이다. 아래는 시그모이드 함수이다. 여기서 z는 앞서 계산한 선형 방정식의 결과이다.
$$\sigma(z) = \frac{1}{1 + e^{-z}}$$
Reference