선형 회귀는 선형 모형(Linear Model)의 한 종류이다. 모든 선형 회귀는 선형 모형이지만, 모든 선형 모형이 선형 회귀는 아님에 유의해야 한다. 선형 모형은 모형식이 파라미터들의 선형 함수로 주어지는 모형을 뜻한다. 다시 말해, $y$와 $x$의 관계가 아니라, $y$와 모수 $\beta$의 관계가 선형이다. 따라서 $x$의 n차항을 포함하는 다항 회귀(Polynomial Regression) 또한 선형 모형에 속한다.
선형 회귀(Linear Regression)
종속 변수와 하나 이상의 독립 변수 간 관계를 모델링하는 통계 기법으로, 독립 변수가 종속 변수에 미치는 영향을 직선의 형태로 설명한다. 아래 예시 이미지를 보자. 2차원 상에 데이터들이 다음과 같이 퍼져 있을 때, 데이터의 경향성을 가장 잘 설명하는 직선을 그릴 수 있다. 이 직선의 방정식을 통해 변수 간 관계를 설명하겠다는 것이 선형 회귀의 기본적인 아이디어다.

종속 변수 $y$와 p개 독립 변수 $(x_{1}, \cdots, x_{p})$에 대한 선형 회귀 모델은 다음과 같이 표현된다.
$$y = \beta_{0} + \beta_{1}x_{1} + \cdots + \beta_{p}x_{p} + \epsilon,\quad \text{where}\; \epsilon \sim^{ind}(0,\sigma^2)$$
- $\beta_{0}$ : 절편(Intercept)으로, 독립 변수 값이 0일 때의 $y$값을 의미
- $\beta_{1}, \cdots, \beta_{p}$ : 회귀 계수(Regression Coefficients)로, 각 독립 변수가 종속 변수에 미치는 영향을 나타냄
- $\epsilon$ : 오차항(Error Term)으로, 실제 데이터와 모델 예측 간의 차이를 설명함
오차항은 $x$와 $y$ 의 관계 바깥에 존재하는, 즉, 모델로 설명할 수 없는 오차를 의미한다. 선형 회귀 모형은 이 오차를 최소화하는 방향으로 모수를 추정한다. 오차의 제곱합을 최소화하는 $\beta$를 구하는 방식을 최소제곱법(Least Squared Method)이라 한다.
계산 과정
최소제곱법은 모델이 예측한 값과 실제 데이터 간의 차이를 최소화하는 방식으로 회귀 계수를 추정한다. 구체적으로, 각 데이터 포인트에 대해 실제 값 $y_{i}$와 모델의 예측 값 $\hat{y_{i}}$의 차이를 잔차(residual)라고 한다. 잔차제곱합(Residual Sum of Squares; RSS)을 최소화하는 것이 선형 회귀 모형의 목표이다. 오차제곱합(Sum of Squared Error; SSE)이라는 표현도 자주 사용된다.
$$ RSS : \sum_{i=1}^{n}(y_{i}-\hat{y_{i}})^2 $$
$$ (y-X\beta)^\top(y-X\beta) =y^\top y-2\beta^\top X^\top y+\beta^\top X^\top X\beta $$
이를 $\beta$에 대해 미분하여 구한 $\hat{\beta}$는 다음과 같다.
$$ \hat{\beta}=(X^\top X)^{-1}X^\top y $$
간단한 모형은 손계산을 통해서도 구할 수 있지만, 구해야 할 모수의 수가 많은 경우에는 기울기하강법 등 수치적 방법을 활용한다.
모형의 기본 가정
선형 회귀 모형은 데이터의 관계를 직선의 형태로 설명하기 위해 여러 가지 강한 가정을 필요로 한다. 이러한 가정이 충족되지 않을 경우, 모형의 유효성이 떨어지고 잘못된 결과를 초래할 수 있다.
- 선형성(Linearity) : 독립 변수와 종속 변수 간 관계가 선형이다.
- 등분산성(Constant Covariance) : 모든 값에 대해 오차항의 분산이 동일하다. 즉, 잔차의 분포가 일정해야 한다.
- 오차의 독립성(No Correlation of Error Term) : 잔차들 사이에 자기상관이 없고, 서로 독립적이다.
선형 회귀 모형의 진단은 잔차플롯으로부터 출발한다. 잔차플롯이란 x축에 예측값을 y축에 잔차(실제값과 예측값의 차이)를 그린 플롯이다. 이 잔차는 앞서 제시한 모형식의 오차항 추정치이므로 모형이 잘 설정되었다면 잔차가 오차항의 가정에 부합할 것이다. 그러므로 잔차가 0을 중심으로 랜덤하게 퍼져 있는지, 눈에 띄는 추세가 없는지 확인한다. 아래 잔차 플롯 예시를 보자. 왼쪽의 잔차는 예측값의 변화에 따라 눈에 띄는 패턴을 가진다. 잔차의 강한 패턴은 데이터의 비선형성을 의미한다.
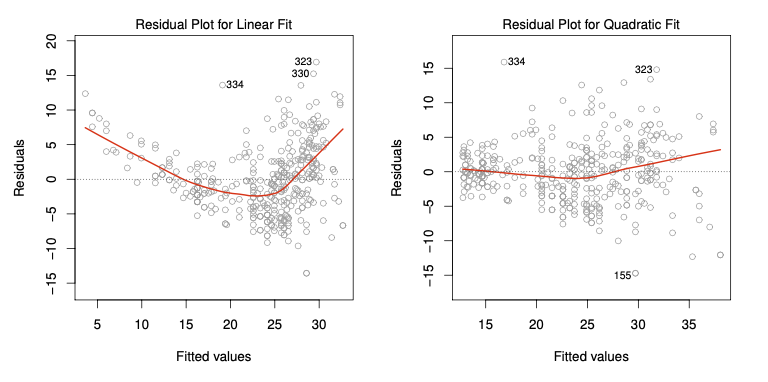
다음으로는 파란색 선에 주목해야 한다. 앞선 예시처럼 예측값의 변화에 따라 잔차가 함께 변화하지는 않지만 잔차의 분포가 커지는 모양을 하고 있다. 이는 데이터의 등분산 가정이 만족하지 않음을 뜻한다. 이러한 경우 변수 변환(Transformation)을 시도할 수 있고, 실제 로그 변환 후 그래프를 보면 분포가 일정하게 나타고 있다.

오차의 독립성의 경우, 더빈-왓슨 검정(Durbin-Watson test)을 통해 검증할 수 있다. 만약 시계열 데이터와 같이 자기상관이 명백한 경우 다른 모형을 고려해야 한다. 모형의 기본 가정은 아니지만 추가적으로 고려해야 할 부분은 다음과 같다.
- 잔차의 정규성(Normality)
잔차의 정규성은 어떤 측면에서는 선형 회귀 모형의 기본 가정으로 볼 수 있다. 회귀 계수 추정에 사용되는 최소제곱법(Ordinary Least Squares; OLS)은 잔차가 정규 분포를 따른다는 가정 하에 유효하기 때문이다. 만약 잔차가 정규 분포를 따르지 않으면, 계수의 추정치가 불안정해진다. 또한 잔차가 정규 분포를 따를 때, 회귀 계수의 신뢰 구간을 정확하게 계산할 수 있고 t-검정이나 F-검정과 같은 가설 검정도 신뢰할 수 있다. 하지만 잔차가 정규성을 따르지 않더라도 회귀 분석 자체는 가능하다. 특히 데이터 크기가 충분히 큰 경우 또는 예측의 정확도가 중요한 경우에는 잔차의 분포가 정규성을 띄지 않더라도 선형 회귀 모형을 활용할 수 있다.
- 공선성(Collinearity)
$(X^\top X)^{-1}$가 존재하기 위해서는 특성변수들이 선형적으로 종속되지 않아야 한다. 다시 말해, 특성변수 간 상관계수가 1이 아니어야 한다. 그러므로 선형 회귀 모형을 적용하는 경우 특성변수 간 다중공선성(Multicollinearity)을 확인하는 과정이 필수적이다. 일반적으로 상관계수의 절댓값이 0.8~0.9 이상이면 두 변수 중 하나를 제외한다.
- 영향점(Influential Points)
회귀 분석에서 특정 데이터 포인트가 회귀 계수에 미치는 영향이 크거나, 잔차(Residual)가 다른 데이터 포인트에 비해 매우 클 경우 이를 영향점이라고 한다. 영향점은 회귀 계수 추정치에 큰 왜곡을 초래할 수 있으며, 이로 인해 모델의 성능이 과대 평가 또는 과소 평가될 수 있다. 따라서 영향점을 사전에 식별하고 필요할 경우 제거하거나 조정하는 방법이 필요하다.
평가(Assessment)
선형 회귀 모형의 성능을 평가하기 위해 여러 지표가 사용된다.
- 결정계수($R^2$, Coefficient of Determination)
종속 변수 $y$의 분산 중 독립 변수 $X$에 의해 설명되는 부분의 비율을 나타낸다. 0에서 1 사이의 값을 가지며, 1에 가까울수록 모형이 데이터를 잘 설명함을 의미한다. 독립 변수의 수가 많을수록 값이 커지기 때문에, 이를 보정한 조정된 결정계수(Adjusted R²)를 사용하기도 한다.
$$R^2 = 1− \frac{SSR}{SST} = 1− \frac{\sum_{i=1}^{n}(y_{i}-\hat{y_{i}})^2 }{\sum_{i=1}^{n}(y_{i}-\bar{y})^2}$$
- 평균 제곱 오차(Mean Squared Error; MSE)
예측값과 실제값 간 차이의 제곱 평균으로, 앞서 소개한 RSS(또는 SSE)의 평균 값이다. MSE가 작을수록 모형의 예측 성능이 더 우수하다고 할 수 있다. 오차의 제곱을 사용하기 때문에 큰 오차에 더 민감하게 반응한다.
$$MSE = \frac{1}{n}\sum_{i=1}^{n}(y_{i}-\hat{y_{i}})^2$$
- 평균 절대 오차(Mean Absolute Error; MAE)
예측값과 실제값 간 차이의 절대값을 평균한 값이다. MSE와 달리 오차를 제곱하지 않으므로 이상치에 덜 민감하다.
$$MAE = \frac{1}{n}\sum_{i=1}^{n}|y_{i}-\hat{y_{i}}|$$
- 평균 절대 백분율 오차(Mean Absolute Percentage Error; MAPE)
예측값과 실제값 간 차이의 절대값을 실제값으로 나눈 백분율을 평균한 값이다. 상대적인 오차를 평가할 수 있기 때문에, 비율로 오차를 확인할 때 유용하다. 단, 실제 값이 0에 가까운 경우 MAPE가 지나치게 커질 수 있다.
$$MAPE = \frac{1}{n}\sum_{i=1}^{n}|\frac{y_{i}-\hat{y_{i}}}{y_{i}}| * 100$$
Reference
Gared James et al., An Introduction to Statistical Learning with Applications in R